Data Blog
샤프지수란? 본문
1. 금융상품의 우열을 가리는 방법
평균 수익률이 높은 운용은 일반적으로 표준편차도 큰 편이다.
즉, 하이 리스크, 하이 리턴 또는 로우 리스크, 로우 리턴이 한 쌍을 이루는 경향이 있다.
이 두 조합 중 어느 쪽이 더 우수하거나 열등하다고 말하기는 어렵다.
이는 단순히 투자자의 선호에 따른 문제일 뿐, 이러한 상품들의 상품성은 본질적으로 동일하다고 볼 수 있다.
같은 직선 위에 있는 금융상품들은 상품성 면에서 우열을 논할 수 없다.
그러나 포트폴리오 A와 같이 상위에 있는 금융상품은 직선 아래의 다른 금융상품들보다 더 우수하며, 반대로 포트폴리오 C와 같이 하위에 있는 금융상품은 상대적으로 열등하다고 볼 수 있다.

2. 금융상품의 우열을 가리는 수치, 샤프지수
샤프지수는 투자 성과를 측정할 때 표준편차를 고려한 지표로, 샤프지수가 클수록 더 우수한 금융상품으로 평가된다.
샤프지수를 계산하는 공식은 다음과 같다. (분자는 리턴을, 분모는 리스크를 평가)
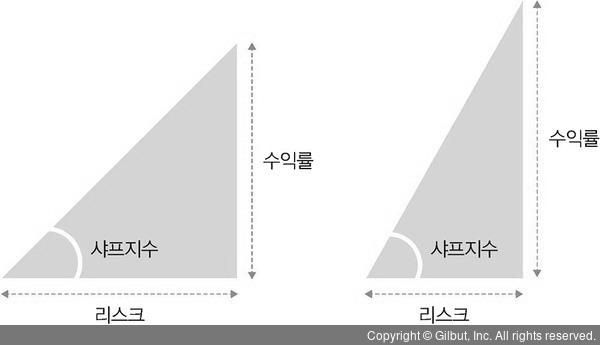
샤프지수가 클수록(각도가 클수록) 리스크 대비 리턴을 잘 운용하는 금융상품이라는 의미가 된다.
X의 샤프지수 = (X의 리턴 - 국채 이자율) ÷ X의 리스크
위 공식에서 국채 이자율(무위험 수익률)을 차감하는 이유는 국채가 누구나 거래할 수 있고, 가장 안전한 이자를 제공하는 자산이기 때문이다. 국가는 기업에 비해 파산 위험이 매우 낮아 국채는 리스크가 적은 금융자산으로 여겨진다.
또한, 국채 이자율을 초과하는 수익을 리스크(표준편차)로 나누는 이유는 리턴이나 리스크가 서로 다른 상품을 비교할 수 있도록 통일된 기준을 제공하기 위해서다.
이전에 언급한 "금융상품에 우열이 없다"라는 표현은 여기에서 샤프지수가 동일하다는 말로 바꿔 표현할 수 있다.
이처럼 투자 및 자산 운용의 세계에서 표준편차는 매우 중요한 지표로 활용된다.
'통계 > 통계학 Statistics' 카테고리의 다른 글
| 표본분산과 비례하는 통계량 W (0) | 2024.10.12 |
|---|---|
| 모분산의 구간 추정 (1) (2) | 2024.10.10 |
| 카이제곱분포 (0) | 2024.10.09 |
| 모평균의 구간 추정 (1) (2) | 2024.10.09 |


